Does increasing pipe size increase water pressure in pipe?

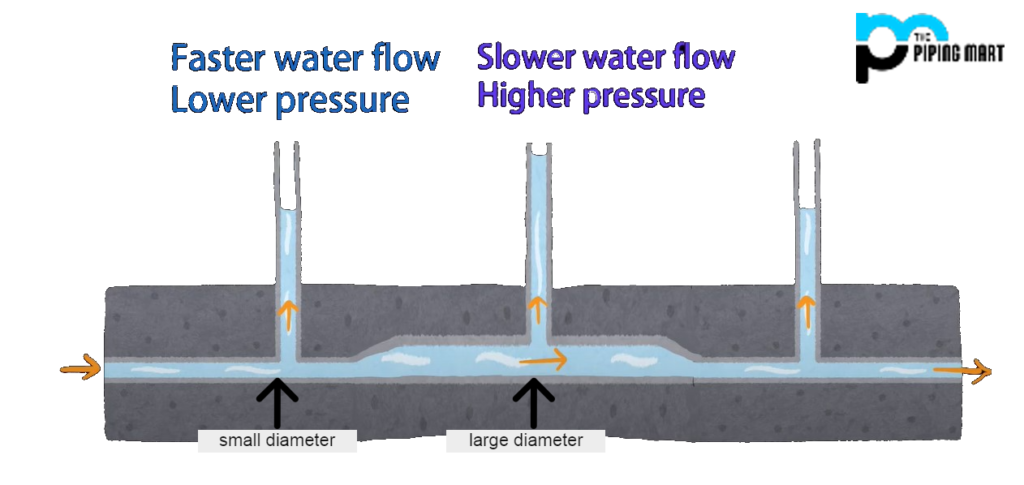
In water-flowing pipelines, size and pressure depend on each other. Because if a diameter decreases, the pressure and amount of water supply in the pipeline will increase. Per Bernoulli’s theorem, pressure can be reduced when the conveyance area is reduced. In the narrower pipe, the speed can be high; hence, the pressure will be lower. Pressure is defined as the force exerted by the liquid per unit area on the walls of the pipe.

Suppose a liquid is passing through a pipe, and the radius of the pipe decreases. In that case, the speed of the fluid rises, the pressure reduces, and the mass flow remains consistent for a period of time till air density is consistent.

 

 

Formulas for flow and pressure (Bernoulli’s equation)

Bernoulli proposed in 1972 – “In a current or stream, if the velocity is low, the pressure is high, the pressure is low when the velocity is high.”

This was the fundamental principle of hydrodynamics before the development of the equations of fluid mechanics and continuous medium theory. Its essence is fluid mechanical energy conservation.

Knowing the equation is derived from mechanical energy conservation is critical. As a result, it applies only to ideal fluids with negligible viscosity and incompressibility.

Bernoulli’s principle is typically stated as follows.

p+1/2ρv2+ρgh=C

This equation is called Bernoulli’s equation.

where

• p is the pressure at a point in the fluid.
• v is the flow velocity of the fluid at that point.
• ρ is the density of the fluid.
• g is the acceleration of gravity.
• h is the height of the point.
• C is a constant.

It can also be expressed as.

p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2

Required Conditions

The solution sought is also an approximation if the following conditions are not fully satisfied.

In the equation context, flow is the amount of fluid passing through a given point over time, expressing the principle of energy conservation in fluid dynamics.

• Steady-state flow

In a flow system, the fluid properties at any point do not change over time.

• Incompressible flow

The density is constant, and the Mach number (Ma) 0.3 applies when the fluid is a gas.

• Frictionless flow

The friction effect is negligible, as is the viscous effect.

• The flow of fluid elements along the streamline

Fluid elements flow along the streamline. The flow lines do not cross.

The Poiseuille’s Law

Flow rate vs pipe size

Poiseuille’s law states that the flow rate through the length of the pipe varies with the fourth power of the radius of the pipe. The length, the liquid’s viscosity, and the pressure to which the liquid is subjected are all variables that affect the flow rate. Poiseuille’s law assumes laminar flow, an idealization that only applies at low water pressures and small pipes. Most real-world applications include turbulence.

The law is expressed as:

Volume flow rate = π X pressure difference X pipe radius 4 X liquid viscosity / 8 X viscosity X pipe length.

F = πPr4 / 8nl

Way to describe, at a given temperature, the flow rate through a tube or pipe is inversely proportional to the tube’s length and the liquid’s viscosity. The flow rate is proportional to the pipe pressure gradient and the fourth power of the pipe radius.

Other factors

The pipe diameter vs flow rate:

In a fluid passing through a pipe, a reduction in the diameter of the pipe can compress the flowing fluid. It flows faster, which increases the greater water flow rate. And with a wider width, there is a lower flow rate. A greater flow rate in a system is often achieved by increasing the pipe diameter, as it allows more fluid to pass through per unit time.

The pipe size and flow:

The water pipe pressure and flow remain the same on both facets of the pipe segment. The rate of water flow is slower in the bigger pipes, but water pressure will increase. In pipes with a small width size, the flow of water is faster than bigger pipes.

The size and water pressure and flow:

The radius decreases, the speed of the fluid rises, and the pressure decreases. The variations in pipe wall size or texture of the pipe will not affect the static pressure. When the connection is open, the water pressure moderately decreases. The larger pipe offers minimum resistance to flow; hence, the pipe’s water pressure is reduced.

Water pressure vs Pipe length:

The reduction in pipe length offers resistance against the flow and also, affects water pressure loss. When the flow velocity increases, the water pressure decreases, and efficiency reduces.

Water flow and water pressure rate:

The water pressure can change the flow rate. If the water pressure in the pipe increases, then the flow rate increases. This equation varies by varying pressure or flow rate and remains constant when these factors remain constant. The difference between water flow and water pressure is that water flow is the amount of water moving through pipes over time, while water pressure represents the force this water exerts on the pipe walls.

Can Pipe Material Affect the Water Pressure in Pipe?

Yes, the material of a pipe at any given time can affect the water pressure and water flow in a pipe. The strength and durability of pipes are essential in determining the stress they can take, and stainless steel pipe is generally considered a good choice for higher water pressure applications. Stainless steel is a strong and durable material that can withstand force exerted without deforming or breaking. However, other materials, such as plastic or aluminium, may need to handle the same amount of pressure level as stainless steel.

 

 

How to Choose a Flow Meter for the Test

• Consistent Flow – As long as there are no leaks or forks in the water line, the flow rate should be consistent throughout. As a result, the flow meter with a water pressure regulator should be installed in areas for a consistent flow stream from a water tower. The higher the water tower, the more force the water will have.
• Flow velocity is inversely proportional to the pipe’s cross-sectional area at any flow rate. Smaller pipes result in faster flow rates, while larger ones result in slower flow rates. As a result, we do not recommend using a small flow or pressure meter on a large pipe. It will be an energy waste, and the speed will be too fast to measure the flow rate.
• The inner diameter will differ between the US and Japanese standard pipe, even for the same size. DN is defined as the outer diameter of a standard pipe. ID could be estimated as the inner diameter of a standard pipe.
• Make any metric or imperial conversions when calculating, if required.  1000ml = 1l; 1mm = 0.001m.

Summary

Increasing the size of your pipes and fittings can increase the water pressure and decrease the speed through which water flow will be increased. This means that water pressure is also on a pipe or fitting is decreased. The larger the diameter and the lower the pressure, the more likely water will flow through your plumbing system. If the amount of water flow is high, the pressure will also increase.

Also Check:

ASTM Specification